|
thermal resistance is a mathematical concept analogous to the electrical resistance we have all studied in basic physics. it is useful to refresh our memory about the electrical resistance before going into describing the thermal resistance.
according to ohm's law, you need a difference in electrical potential in order to produce current. mr. george simon ohm (1787-1854) established the fundamental relationship between voltage, current and resistance in an electrical circuit. indeed, ohm's law, simply put is:
ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points. introducing the constant of proportionality, the resistance, one arrives at the usual mathematical equation that describes this relationship:
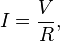
where i is the current through the conductor in units of amperes, v is the potential difference measured across the conductor in units of volts, and r is the resistance of the conductor in units of ohms. more specifically, ohm's law states that the r in this relation is constant, independent of the current.
the constant of proportionality is defined as electrical resistance between the two points
please notice that in the simple configuration shown above you are nor worried about losing the electric current to the ambient as it passes through the wire. what starts at one end shows up at the other end because air is a terrible conductor for electricity.
now, let's look at a one dimensional conduction problem:
remember that we put a "one-dimensional" constraint on the problem. a problem is considered one dimensional if things happen only along one dimension. this means that we are assuming that the heat going from the left side to the right side does not escape to the ambient. well, the only way to do this is if we insulate the surface of our wire using a perfect insulator. in that case we end up with a consistent definition for the thermal resistance because all of our q goes from t1 to t2.
now, let's take a look at a two dimensional situation: if the left face is all at a uniform temperature of t1 and the right face is at the uniform temperature of t2 and all other faces are perfectly insulated then we have a one dimensional situation. however, if somewhere between the right hand face and the left hand face, the heat has a way to go out, then we are dealing with a 2d or a 3d case:
now, how do you define the thermal resistance for this object? which points do you take for your t2? what q do you use? the total q or the q that goes from t1 to t2? how do you measure that?
has this simple problem stopped people from using the thermal resistance as a measure of heat transfer friendliness? no. it has not. why? because the concept is still very useful figure of merit if you know how to use it.
is high thermal resistance good or bad? the answer depends on whether your are trying to get rid of heat or you want to keep the heat. if you are trying to keep something cool by rejecting its heat, you want really low thermal resistance. if your are trying to keep what you have you want high thermal resistance. i would like to have a very high thermal resistance for my walls at home so that i can save energy.
however, if i am trying to keep a chip cool, i need to reduce all thermal resistances that prevent the heat from leaving my precious components.what is high value of thermal resistance? if i tell you that i have a heat sink with a thermal resistance of 0.5 degree c/w, is that good or bad? how bad? what does this number mean? this latter question is actually very simple to answer.
a resistance of 0.5 degree c/w means that if one watt of heat goes through the object, the temperature drops by 0.5 degrees. let's look at a block of aluminum with a length of 2 cm and a cross-sectional area of 2 cm x 2 cm. a quick calculation tells us that the value of r is:
(2x0.01 m)/(180 w/m.c x 4x0.0001)= 0.27 degree c/w
if we use copper instead of aluminum, the resistance drops to 0.125 degree c/w.
in practical applications, the conduction resistance isn't the only resistance your have to fight. the next big resistance is due to convection. even if the heat works really hard or you use a very high conductivity material, it still has to go through the air in order to be completely rejected. there is this very thin layer of air (or the working fluid) right at the surface of the solid object that shows the greatest resistance to the heat transfer. this first layer of the air actually sticks to the surface and does not move. the other layers slide over this first layer and can take the heat away. this layer is called the boundary layer.
there are some intuitive things we all know about removing heat by convection. if we move the fluid faster, we can carry more heat away. if we use a more thermally conductive fluid, we take more heat off. if we create turbulence which mixes things up pretty good, we can take more heat away from the surface. the convective resistance is related to a parameter called heat transfer coefficient. defining and understanding this important parameter requires another tutorial. here is suffices to just use the newton's law of cooling:
q= h.a. (ts-ta)
where h is the heat transfer coefficient, a is the surface area, ts is the surface temperature and ta is the reference temperature. by rearranging the equation we see a familiar format:
q= (ts-ta)/(1/ha)
q= (ts-ta)/rconv
where rconv = 1/ha
this means that if you are looking at an electronic component, for example, the heat must overcome at least two resistances before it can reach the ambient. the first resistance is from the location of the heat generation to the surface and the second one is from the surface to the ambient. when you use a more conductive material, you are only dealing with the first resistance. to reduce the second resistance, you must deal with h. enough about h for now as we will deal with it in a separate tutorial.
other types of thermal resistance
we talked about conduction and convection but there are other sources of resistance to the flow of heat. here we briefly touch upon them as they are separate topics for our future tutorials.
contact resistance
whenever you attach two objects together, you end up with a thermal resistance due to the fact that these surfaces are never smooth (no matter how much you polish them). in reality each surface is like a bunch of hills and valleys. only the tip of hills from each surface has a chance of really touching the other surface. the rest is filled with air (or whatever fluid this thing is immersed in). the common way of reducing this resistance is to fill the gap with a material with good thermal conductivity and then either apply a lot of pressure and/or use a material that cures in place and fills those gaps for you.
spreading resistance
when heat wants to go from a small area to a larger area, it has to do some work. it is like you are forcing the heat to bend and deviate from the the straight path it always prefers to take. it will give you resistance. this is spreading resistance.
putting them together
let's look at the all resistance elements when the heat generated inside an ic is trying to get out into the ambient.
the heat produced at the junction will either go through the air (which is not very easy because air is a terrible heat conductor) or through the chip (the blue block). note that the junction area is less than the chip area which implies that we will have a spreading resistance here. there is, of course, the material resistance of the chip itself. the chip is attached to the lead frame by some sort of epoxy.
here we assume that the bond is perfectly attached to the chip and the lead frame. the heat may experience another spreading resistance if the contact area between the bond and the lead frame is smaller than the surface area of the lead frame. from the lead frame, the heat has to first go into the case and then turn around and go into the leads. all along, there is heat transfer between the leads and the case (while the case itself is engaged in exchanging heat with its ambient).
once the lead comes out of the package, it is exposed to the ambient and starts its own exchange. the heat then goes into the board and travels through it while exchanging energy with the ambient surrounding the board.
in practice, two lumped resistance elements are associated with a package. the set of resistances we talked about in the last paragraph is lumped into junction-to-board thermal resistance. the resistance from the junction to the outer surface of the case is called junction-to case resistance. when convection is taken into account, we often use another resistance called junction-to-ambient resistance. when a heat sink is attached to the case, then we add two new terms, case-to-sink and sink-to-air resistances. the latter is what heat sink manufacturers publish as the characteristic of their heat sinks.
what is important to notice here is that these lumped resistances are actually composed of many complex heat transfer mechanisms. using these measures of component characteristic in a casual way without understanding the physics is dangerous and may lead to erroneous conclusions.
please remember that most of these parameters are measured under a specific set of conditions. before using these numbers and betting your designs on them make sure that your operating conditions are similar to those used for the characterization.
|