introduction

most high-powered electronic devices are cooled by forced convection airflow, but occasionally there is a need for natural convection cooling. determining factors, which include cost, noise, vibration and reliability, can eliminate use of a fan or blower – particularly in consumer electronics and outdoor enclosures. fan failure will also change the flow regime from forced flow to natural convection. in contrast with airflow generated by the mechanical working of a prime air mover, natural convection results from the buoyancy forces generated by the ambient air being heated by a heat source. air adjacent to the heat source absorbs heat from the surface, becomes hotter than the surrounding air, and rises due to density differences. cooler air displaces the warmer air and a natural convection flow thus develops. the magnitude of the airflow depends on the solid geometry, surface heat flux and the buoyancy characteristics of the carrying fluid – as determined by the dimensionless rayleigh number.

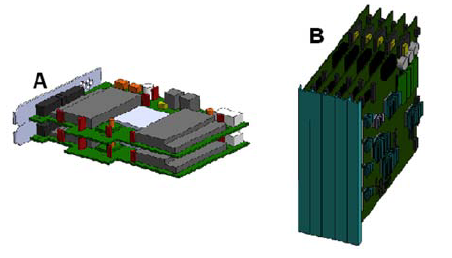
figure 1. common orientation of electronics boards

the geometry of a heat source plays an important role in determining heat transfer characteristics. consider a power consuming chip on a circuit board: the orientation of the board relative to the direction of gravity can have a large effect on cooling the chip via natural convection. an adapted form of ellison’s[1] model can be used for simplified configurations, as shown below in figure 1, to predict the local heat transfer coefficient for a specific heat source per a specific orientation relative to the direction of gravity.

figure 1 presents two common configurations of electronics boards. example a is a set of pci express cards which are stacked along the vector of gravity, so that the boards are perpendicular to gravity. example b shows a stack of atca boards which aligned parallel to gravity.  where:

table 1.  table of parameters used in ellison's analytical model [1].

for maximum heat transfer in applications where the desired cooling method is natural convection, boards with power dissipating devices should be stacked in the vertical plane. packing boards in the vertical direction increases the spatial consolidation of the boards and increases heat transfer per unit area due to optimized natural convection.

for a single plate suspended in the vertical configuration, the resulting velocity profile will be parabolic. there is no interference with any other disturbances; the only controllable variables are adjusting the height, width and power of the board. when multiple boards are stacked to create vertical channels, the velocity profiles interact. their interaction is a function of the spacing, or channel width, between the boards. figure 2 is an adapted graph showing the heat dissipation of a set of two parallel isothermal plates as a function of channel width at a temperature difference of 20°c and a constant board area of 0.078m2. a and b are design points where the slope of the line connecting to the origin represents the amount of power per unit of channel width. point b is shown to have a maximum slope, which represents the maximum possible packing density for a particular configuration. in order to maximize power density for isothermal boards, an engineer should aim to design for point b. note that past the optimum and toward point a there is no longer any potential gain in power consumption as the channels are widened.

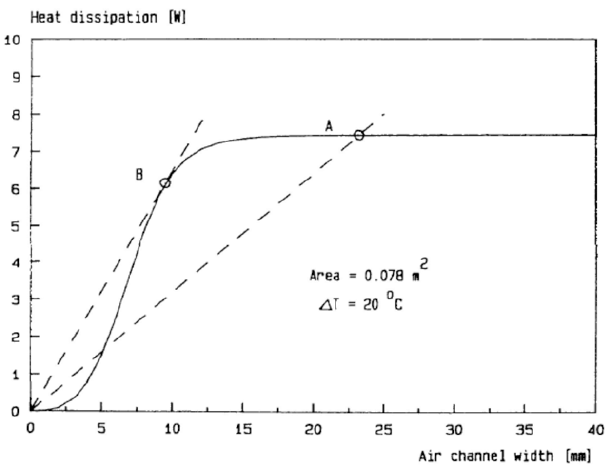
figure 2. heat dissipation from isothermal boards as a function of board spacing in natural convection [2]

the relationship discerning board optimization for isothermal boards can be described [2] as:

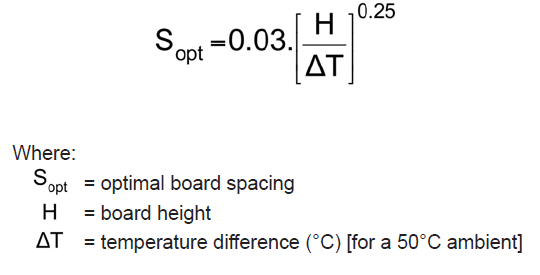
for the configuration of two isothermal plates, the average nusselt number across a plate can be described by the following equation [3]:

for a channel between two plates with equal heat flux, the hottest -- and thus the most critical point of interest -- rests at the end of the board nearest the exhaust of the channel. in this particular configuration, the optimal spacing can be defined as [3]  where:

likewise, a calculation for the local heat transfer coefficient at the end of a set of plates with uniform heat flux can be found as [3]:

the above equations are useful for calculating initial and simplistic results based on viable assumptions. a stack of boards can often be modeled as plates where there are less significant heat source points or protrusions from the board, or where the thermal conductivity of the board is high enough to assume isothermal characteristics. for some cases, memory modules aligned in channel-like configurations can be modeled as a set of plates with uniform heat flux - the heat transfer characteristics can be estimated from the above correlations. similarly, the fins of a heat sink in natural convection can be modeled as isothermal plates which create channels. for most heat sinks, their material conductivity is high enough to negate any significant temperature gradients along the fins.

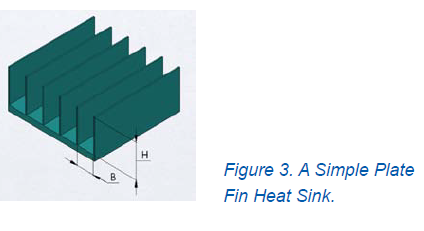
for a generic plate fin heat sink, with a fin height of h, and spacing between fins of b, there is a relative fin spacing to fin length ratio which will provide optimal heat transfer within a given volume. where spatial constraints prevent the use of a larger sized heat sink, optimizing its design for natural convection and increasing its efficiency can be the difference between normal operation and thermal failure. 

because the heat sink has to include heat transfer from the base, an equivalent channel width needs to be determined.  the equivalent channel width is solved similar to a hydraulic diameter, as seen below [2].

the heat extracted from the heat sink can be found using this equivalent channel width and an assumed temperature difference between the ambient and heat sink surface.  the results shown in figure 4 highlight the effects of changing the fin height relative to fin to fin spacing. for low volumes, it may not be economical to extrude or machine a heat sink with the exact geometry to optimize heat transfer from a given control volume, but the results show that for a standard or offthe-shelf solution it is safer to pursue a design with a larger fin spacing to fin height ratio than otherwise.

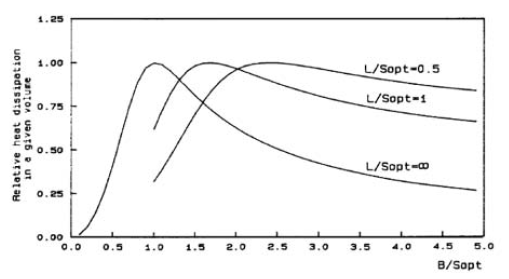
in this article we have shown that many applications prevent the use of forced convective flow from fans or other sources, due to acoustics, cost or other reasons. but, optimizing heat transfer by using the natural buoyancy-induced movement of air can be effective in cooling electronics. some techniques for optimizing airflow and heat transfer in natural convection situations involve a vertical channel. for heat-generating boards suspended in a vertical configuration, there is calculable board spacing which will lead to an optimal power density per volume. heat sinks can also be optimized for natural convection, and while it may not be feasible to obtain a heat sink of the perfect fin height and fin pitch for a workable volume, the next best performer is a heat sink with larger fin spacing relative to fin height.

references:

1. hwang, p., cheng, h., fang, j. and li, j., cfd-based thermal characterization of board-level microelectronic devices under natural convection cooling, microsystems, packaging, assembly and circuits technology, 2007. impact 2007.

2. malhammar, a., optimum sized air channels for natural convection cooling, telecommunications energy conference, 1987.

3. incropera, f., liquid cooling of electronic devices by single phase convection. new york, wiley. 1999.